Coordinate Representation
Normally,
graphics packages required coordinate specifications to be given with respect
to coordinate reference frames.
To
describe a picture, the world-coordinate reference frame (2D or 3D) must be
selected.
Rene Descartes, the French mathematician, and philosopher,
discovered that some algebraic equations could be interpreted geometrically by
graphing them onto a two-dimensional coordinate system. He had founded analytic
geometry. The rectangular, two- dimensional system he used to graph algebraic
functions bears his name Cartesian co-ordinate system.
Figure
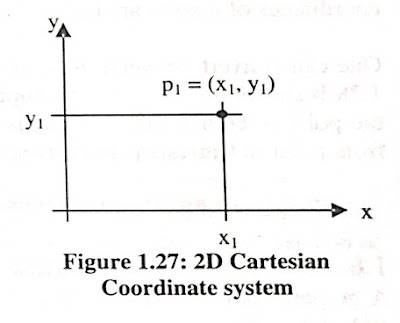
1.27: 2D Cartesian Coordinate system
The two-dimensional
Cartesian coordinate system has well-defined properties. To construct two-dimensional Cartesian coordinate system one has to use two (hypothetically)
unbounded straight lines intersecting at right angles to form the Principal
axes x and y, with positive and negative directions. indicated (ligure 1.27).
Their point of intersection O is the origin. One imposes a grid of equally
spaced lines parallel to and in the plane of the principal axes, which forms
the basis of all measurements and analysis. Every point in the plane of uns
coordinate system is defined by a pair of numbers (x, y), its coordinates.
The
coordinates of p, in the figure are (X1, Y1). To locate pi in the system, we construct
a line parallel to the y axis through x1, and parallel to the x axis through
y1. These two lines intersect at p1.
The
location and orientation of a coordinate system are arbitrary, and there may be
more than one.
The polar
coordinate system has limited use in computer graphics and geometric
modeling, but its relationship to the Cartesian system suggests how he/she
might rotate points. Figure 1.28 a illustrates a polar coordinate system:
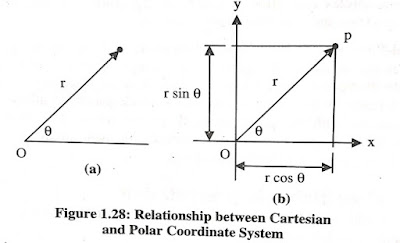
Figure 1.28: Relationship between Cartesian and Polar
Coordinate System
Points
in it are located by giving their distance r from the origin and the angular
displacement of the line of r
with respect to a reference line. Thus, the polar coordinates of a point are
(r,
One can
convert between polar coordinates and Cartesian coordinates. Figure 1.28 b
shows the two systems superimposed so that their origins coincide and the polar
reference line and x axis are collinear. The transformation equations from
polar to Cartesian are derived using simple trigonometry. Thus,
x = r
cos
y =r
sin
Screen Coordinates
A graphics device has a “screen” (possibly a piece of
paper) of specified size and shape. Most of screens are rectangular and are
described by a “pixel” coordinate system which labels the rows and columns of
the screen. These row and column coordinates will be called screen, device or
display coordinates.
Computer
screens typically use a coordinate system which also consists of an origin and
two axes, at right angles to each other, intersecting at a point called the
origin.
Each
point on the plane containing the coordinates is uniquely identified by two
numbers:
1) The
first represents the signed horizontal distance from the vertical axis, and